인공 신경망(Aritificial Neural Network-ANN)
- 생물학적 뉴런에서 영감을 받아 만든 머신러닝 알고리즘
- 이미지, 음성, 텍스트 분야에서 뛰어난 성능 발휘
- 딥러닝 이라고도 불림
- 기본적으로 로지스틱 회귀(SGDClassifier)와 비슷
01. 머신 러닝 용어
1. 머신 러닝 모델의 평가
실제 모델을 평가하기 위해 데이터를 훈련, 검증, 테스트용 세가지로 분리하는 것이 일반적
- 검증용 데이터 : 모델의 성능을 조정하기 위한 용도, 과적합 판단이나 하이퍼파라미터 조정을 하는데 쓰임
- 하이퍼파라미터 : 모델의 성능에 영향을 주는 사용자가 직접 정해줄 수 있는 변수
ex) learning rate, 히든레이어의 수, 뉴런 수, 드롭아웃 비율 등
- 튜닝 - 훈련용 데이터로 훈련을 시킨 모델을 검증용 데이터를 사용해 정확도를 검증하며 하이퍼 파라미터를 조정
- 모델에 대한 최종 평가 : 검증용 데이터는 모델이 일정부분 최적화되기 때문에 테스트 데이터로 수행
2. 분류(Classification)와 회귀(Regression)
대부분의 머신러닝 문제는 분류나 회귀에 속함
- 이진 분류(Binary Classification) : 주어진 입력에 대해 둘 중 하나의 답을 정하는 문제
- 다중 클래스 분류( Multi-class Classification) : 주어진 입력에 대해 세 개 이상의 선택지 중 답을 정하는 문제
- 회귀 문제(Regression) : 연속된 값을 결과로 가짐 ex) 주가 예측, 생산량 예측, 지수 예측 등
3. 지도 학습과 비지도 학습
- 지도 학습 : 정답(레이블)과 함께 학습
- 비지도 학습 : 정답(레이블)이 없는 학습 방법 ex) 군집(clustering)이나 차원 축소
- 강화 학습 : 어떤 환경 내에서 정의된 에이전트가 현재의 상태를 인식하여 선택 가능한 행동들 중 보상을 최대화하는 행동이나 순서를 선택함
4. 샘플(Sample)과 특성(Feature)
대부분의 머신 러닝 문제는 1개 이상의 독립 변수 x를 가지고 종속 변수 y를 예측하는 문제임
- 샘플 : 하나의 데이터, 하나의 행을 샘플이라 부름(실물)
- 특성 : 종속 변수 y를 예측하기 위한 각각의 독립 변수 x를 특성이라 부름(성격)
5. 혼동 행렬(confusion Matrix)
정확도(Accuracy - 맞춘 문제수를 전체 문제수로 나눈 값)는 맞춘 결과나 틀린 결과에 대해 세부적인 내용을 알려주진 않음, 이 내용을 알기 위해 사용되는 행렬
| 참 | 거짓 | |
| 참 | TP(정답/정답일꺼야) | FN(오답/오답일꺼야) |
| 거짓 | FP(오답/정답일꺼야) | TN(정답/오답일꺼야) |
- 정밀도(Precission) : TP / (TP + FP) 의 비율, 정답이라고 추측한 전체 케이스에 대한 TP의 비율
- 재현율(Recall) : TP / (TP + FN) 의 비율, 정답(실제값)인 데이터의 전체 개수에 대한 TP의 비율
6. 과적합(Overfitting)과 과소적합(Underfitting)
- 과적합 : 훈련 데이터를 과하게 학습해 테스트 데이터나 실제 서비스에서 정확도가 좋지 않는 경우
- 과소적합 : 테스트 데이터의 성능이 올라갈 여지가 있는데 훈련을 덜 한 상태, 훈련 데이터에 대해서도 정확도가 낮음
* 과적합을 막기 위한 방법 : Dropout, Early Stopping 등
02. 퍼셉트론(Perceptron)
1. 퍼셉트론
- 초기형태의 인공 신경망, 다수의 입력으로 부터 하나의 결과를 내보내는 알고리즘
2. 단층 퍼셉트론(Single-Layer Perceptron)
- 입력층(input layer)과 출력층(output layer) 둘로만 이루어짐
- 단층 퍼셉트론은 AND, NAND, OR 게이트를 쉽게 구현 가능
- AND 게이트 구현 예(두 개의 입력값이 1인 경우에만 1을 출력)
# AND 게이트 구현 예
def AND_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = -0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
# 오직 두개의 입력값이 1인 경우에만 1을 출력
AND_gate(0,0),AND_gate(0,1),AND_gate(1,0),AND_gate(1,1)
- NAND 게이트 구현 예(두 개의 입력값이 1인 경우에만 0이 출력)
# NAND 게이트 구현 예
def NAND_gate(x1, x2):
w1=-0.5
w2=-0.5
b=0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
# 두개의 입력값이 1인 경우에만 0이 나옴
NAND_gate(0, 0), NAND_gate(0, 1), NAND_gate(1, 0), NAND_gate(1, 1)
- OR 게이트 구현 예(두 개의 입력값 중 하나가 1이 들어가면 1을 출력)
# OR 게이트 구현 예
def OR_gate(x1, x2):
w1=0.6
w2=0.6
b=-0.5
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
# 두개의 입력값 중 하나가 1이 들어가면 1이 출력
OR_gate(0, 0), OR_gate(0, 1), OR_gate(1, 0), OR_gate(1, 1)
3. 다층 퍼셉트론(MultiLayer Perceptron, MLP)
- 다층 퍼셉트론은 입력층과 출력층 사이에 층을 하나 더 추가함, 이 층을 은닉층(hidden layer)라 부름
- XOR을 구현 가능
- 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN)이라 부르고 DNN으로 학습하는 것을 딥 러닝(Deep Learning)이라 부름
- XOR 게이트 구현 예(두 개의 입력값이 서로 다른 값을 갖고 있을 때만 출력값이 1이 되고 나머지는 0이 됨)
# XOR 게이트 구현 예
def XOR_gate(x1, x2):
w1=0.6
w2=0.6
b=-0.5
result = x1*w1 + x2*w2 + b
if result <= 0:
return AND_gate(x1, x2) # 층을 하나 더 추가함으로 XOR 게이트를 구현 가능
else:
return NAND_gate(x1, x2)
# 두개의 입력값이 서로 다른 값을 갖고 있을 때만 출력값이 1이 되고 나머진 0이 됨
XOR_gate(0, 0), XOR_gate(0, 1), XOR_gate(1, 0), XOR_gate(1, 1)
03. XOR 단층 퍼셉트론 구현
1. 파이토치로 단층 퍼셉트론 구현
# 도구 임포트
import torch
import torch.nn as nn
# GPU 연산이 가능할 경우 GPU 연산 수행
device = 'cuda' if torch.cuda.is_available() else 'cpu'
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# XOR 문제에 해당하는 입력과 출력 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)
# 1개의 뉴런을 가지는 단층 퍼셉트론 구현, 활성화 함수로 시그모이드 함수 사용
linear = nn.Linear(2, 1, bias=True)
sigmoid = nn.Sigmoid()
model = nn.Sequential(linear, sigmoid).to(device)
# 이진 분류 문제이므로 비용 함수로 크로스엔트로피 함수 사용
# nn.BCELoss() - 이진 분류에서 사용하는 크로스엔트로피 함수
# 비용 함수와 옵티마이저 정의
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)
# 훈련 수행
#10,001번의 에포크 수행. 0번 에포크부터 10,000번 에포크까지.
for step in range(10001):
optimizer.zero_grad()
hypothesis = model(X)
# 비용 함수
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
if step % 100 == 0: # 100번째 에포크마다 비용 출력
print(step, cost.item())
- 마지막 에포크까지 비용이 줄지 않음, 단층 퍼셉트론은 XOR 문제를 풀 수 없기 때문
2. 학습된 단층 퍼셉트론의 예측값 확인
with torch.no_grad():
hypothesis = model(X)
predicted = (hypothesis > 0.5).float()
accuracy = (predicted == Y).float().mean()
print('모델의 출력값(Hypothesis): ', hypothesis.detach().cpu().numpy())
print('모델의 예측값(Predicted): ', predicted.detach().cpu().numpy())
print('실제값(Y): ', Y.cpu().numpy())
print('정확도(Accuracy): ', accuracy.item())
- 실제값이 0, 1, 1, 0 임에도 예측값은 0,0,0,0 으로 문제를 풀지 못함
04. XOR 다층 퍼셉트론 구현
1. 파이토치로 다층 퍼셉트론 구현
# 도구 임포트
import torch
import torch.nn as nn
# GPU 설정 및 랜덤 시드 고정
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# XOR 문제를 풀기 위한 입력과 출력 정의
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)
# 다층 퍼셉트론 설계. 입력층, 은닉층1, 은닉층2, 은닉층3, 출력층을 가지는 인공신경망
model = nn.Sequential(
nn.Linear(2, 10, bias=True), # input_layer = 2, hidden_layer1 = 10
nn.Sigmoid(),
nn.Linear(10, 10, bias=True), # hidden_layer1 = 10, hidden_layer2 = 10
nn.Sigmoid(),
nn.Linear(10, 10, bias=True), # hidden_layer2 = 10, hidden_layer3 = 10
nn.Sigmoid(),
nn.Linear(10, 1, bias=True), # hidden_layer3 = 10, output_layer = 1
nn.Sigmoid()
).to(device)
# 비용 함수와 옵티마이저 선언
# nn.BCELoss() - 이진 분류에서 사용하는 크로스엔트로피 함수
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1) # modified learning rate from 0.1 to 1
# 훈련 수행. 각 에포크마다 역전파 수행
for epoch in range(10001):
optimizer.zero_grad()
# forward 연산
hypothesis = model(X)
# 비용 함수
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
# 100의 배수에 해당되는 에포크마다 비용을 출력
if epoch % 100 == 0:
print(epoch, cost.item())
- 마지막 에포크를 보면 비용이 준 것을 확인
2. 학습된 다층 퍼셉트론의 예측값 확인
with torch.no_grad():
hypothesis = model(X)
predicted = (hypothesis > 0.5).float()
accuracy = (predicted == Y).float().mean()
print('모델의 출력값(Hypothesis): ', hypothesis.detach().cpu().numpy())
print('모델의 예측값(Predicted): ', predicted.detach().cpu().numpy())
print('실제값(Y): ', Y.cpu().numpy())
print('정확도(Accuracy): ', accuracy.item())
05. 비선형 활성화 함수(Activation function)
- 비선형 활성화 함수 : 입력을 받아 수학적 변환을 수행하고 출력을 생성하는 함수
1. 활성화 함수의 특징 - 비선형 함수(Nunlinear function)
- 활성화 함수는 선형 함수가 아닌 비선형 함수다
- 비선형 함수는 직선 1개로는 그릴 수 없는 함수를 말함
* 인공 신경망의 능력을 높이기 위해 은닉층을 계속 추가해야하는 경우 활성화 함수로 선형 함수를 사용하게 되면 은닉층을 쌓을 수가 없음. 기울기 자체가 변동이 없기 때문
2. 시그모이드 함수(Sigmoid function)와 기울기 소실
import numpy as np # 넘파이 사용
import matplotlib.pyplot as plt # 맷플롯립 사용
# 시그모이드 함수 그래프를 그리는 코드
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
- 시그모이드 함수 그래프를 보면 출력값이 0 또는 1에 가까워지면 그래프의 기울기가 완만해짐
- 기울기 소실 문제 : 역전파 과정에서 0에 가까운 아주 작은 기울기가 곱해지면, 앞단에는 기울기가 잘 전달되지 않는 현상
- 시그모이드 함수를 사용하는 은닉층의 개수가 다수가 되면 0에 가까운 기울기가 계속 곱해짐, 이는 앞단에서는 거의 기울기를 전파받을 수 없고, 매개변수 W가 업데이트 되지 않아 학습이 되지 않음
- 결론적으로 시그모이드 함수를 은닉층에서 사용하는 것은 지양됨
3. 하이퍼볼릭탄젠트 함수(Hyperbolic tangent function)
- 하이퍼볼릭탄젠트 함수(tanh)는 입력값을 -1 과 1 사이로 변환
x = np.arange(-5.0, 5.0, 0.1) # -5.0부터 5.0까지 0.1 간격 생성
y = np.tanh(x)
plt.plot(x, y)
plt.plot([0,0],[1.0,-1.0], ':')
plt.axhline(y=0, color='orange', linestyle='--')
plt.title('Tanh Function')
plt.show()
- 하이퍼볼릭 함수도 -1과 1에 가까워지면 시그모이드와 같은 문제가 발생하지만 시그모이드와 달리 0을 중심으로 기울기 폭이 큼
4. 렐루 함수(ReLU)
할렐루야, 인공 신경망에서 최고의 인기를 얻고 있는 함수
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.plot([0,0],[5.0,0.0], ':')
plt.title('Relu Function')
plt.show()
- 렐루 함수는 음수를 입력하면 0을 출력하고, 양수를 입력하면 입력값을 그대로 반환
- 특정 양수값에 수렴하지 않음으로 심층 신경망에서 시그모이드 함수보다 훨씬 잘 작동
- 시그모이드 나 하이퍼볼릭탄젠트 함수와 달리 단순 임계값이므로 연산 속도가 빠름
- 입력값이 음수면 기울기도 0이 됨, 이것을 죽은 렐루(dying ReLU)라고 함
5. 리키 렐루(Leaky ReLU)
- 죽은 렐루를 보완하기 위한 ReLU 변형 함수
- 입력값이 음수일 경우 0이 아니라 0.001과 같은 매우 작은 수를 반환하도록 설계
a = 0.1
def leaky_relu(x):
return np.maximum(a*x, x)
x = np.arange(-5.0, 5.0, 0.1)
y = leaky_relu(x)
plt.plot(x, y)
plt.plot([0,0],[5.0,0.0], ':')
plt.title('Leaky ReLU Function')
plt.show()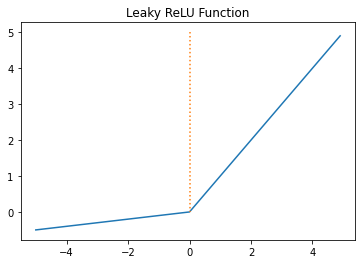
- 위와 같이 입력갑싱 음수라도 기울기가 0이 되지 않으면 ReLU는 죽지 않음
6. 소프트맥스 함수(Softmax Function)
- 은닉층에서 렐루나 리키렐루 함수들을 사용하는 것이 일반적이지만 시그모이드 함수나 소프트맥스 함수가 사용되기도 함
- 분류 문제를 로지스틱 회귀와 소프트맥스 회귀를 출력층에 적용하여 사용
x = np.arange(-5.0, 5.0, 0.1) # -5.0부터 5.0까지 0.1 간격 생성
y = np.exp(x) / np.sum(np.exp(x))
plt.plot(x, y)
plt.title('Softmax Function')
plt.show()
- 소프트맥스 함수는 출력층의 뉴런에서 주로 사용됨
- 시그모이드 함수가 이진 분류에 사용된다면 다중 분류에는 소프트 맥스 함수가 주로 사용됨
7. 출력층의 활성화 함수와 오차 함수와의 관계
| 문제 | 활성화 함수 | 비용 함수 |
| 이진 분류 | 시그모이드 | nn.BCELoss() |
| 다중 클래스 분류 | 소프트맥스 | nn.CrossEntropyLoss() |
| 회귀 | 없음 | MSE |
- 스탠포드 대학교의 딥러닝 강의에선 ReLU, ReLU 변형함수 순으로 사용을 권장하며 sigmoid는 사용하지 말것을 권장
07. 다층 퍼셉트론으로 손글씨 분류
1. 숫자 필기 데이터
- 숫자 필기 데이터는 사이킷런 패키지의 분류용 예제 데이터
- 0부터 9까지의 숫자를 손으로 쓴 이미지 데이터
- 각 이미지는 0부터 15까지의 라벨을 가지는 8x8=64 픽셀의 흑백 이미지로 1, 797개로 구성
# load_digits()를 통해 이미지 데이터 로드
%matplotlib inline
import matplotlib.pyplot as plt # 시각화를 위한 맷플롯립
from sklearn.datasets import load_digits
digits = load_digits() # 1,979개의 이미지 데이터 로드
# 첫번째 샘플 출력, 0을 흰색, 0보다 큰 숫자를 검은색 점이라고 볼 수 있음
print(digits.images[0])
# 첫번째 샘플의 레이블 확인
print(digits.target[0])
# 전체 샘플 갯수 확인
print('전체 샘플의 수 : {}'.format(len(digits.images)))
# 전체 샘플 중 상위 5개의 샘플만 시각화
images_and_labels = list(zip(digits.images, digits.target))
for index, (image, label) in enumerate(images_and_labels[:5]): # 5개의 샘플만 출력
plt.subplot(2, 5, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('sample: %i' % label)
# 상위 5개의 레이블 확인
for i in range(5):
print(i,'번 인덱스 샘플의 레이블 : ',digits.target[i])
훈련 데이터 레이블을 각각 X, Y 에 저장
- digits.images : 모든 샘플을 8x8 행렬로 저장
- digits.data : 8x8 행렬을 전무 64차원의 벡터로 변환해서 저장된 상태
# digits.data를 이용해 첫번째 샘플 출력
print(digits.data[0])
# data를 X 에 저장하고 레이블을 Y에 저장
X = digits.data # 이미지. 즉, 특성 행렬
Y = digits.target # 각 이미지에 대한 레이블
2. 다층 퍼셉트론 분류기 생성
# 도구 임포트
import torch
import torch.nn as nn
from torch import optim
# 모델 정의
model = nn.Sequential(
nn.Linear(64, 32), # input_layer = 64, hidden_layer1 = 32
nn.ReLU(),
nn.Linear(32, 16), # hidden_layer2 = 32, hidden_layer3 = 16
nn.ReLU(),
nn.Linear(16, 10) # hidden_layer3 = 16, output_layer = 10
)
# 데이터 로드
X = torch.tensor(X, dtype=torch.float32)
Y = torch.tensor(Y, dtype=torch.int64)
# 비용함수 정의
loss_fn = nn.CrossEntropyLoss() # 이 비용 함수는 소프트맥스 함수를 포함하고 있음.
# 옵티마이저 정의
optimizer = optim.Adam(model.parameters())
# 손실값
losses = []
# 훈련 실행
for epoch in range(100):
optimizer.zero_grad()
y_pred = model(X) # forwar 연산
loss = loss_fn(y_pred, Y)
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, 100, loss.item()
))
losses.append(loss.item())
# 손실값 확인
plt.plot(losses)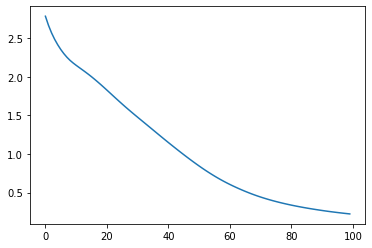
# 모델 테스트
import random
r = random.randint(0, len(X) - 1)
index = r
model.eval()
data = X[index]
output = model(data)
_, predicted = torch.max(output.data, 0)
print("예측 결과 : {}".format(predicted))
X_test_show = (X[index]).numpy()
plt.imshow(X_test_show.reshape(8, 8), cmap='gray')
print("이 이미지 데이터의 정답 레이블은 {:.0f}입니다".format(Y[index]))
08. 과적합(Overfitting)을 막는 방법들
- 모델이 과적합 되면 훈련 데이터에 대한 정확도는 높을지라도, 새로운 데이터, 검증데이터나 테스트 데이터에 대해 제대로 동작하지 않는다.
1. 데이터의 양을 늘린다.
- 데이터의 양을 늘릴 수록 모델은 데이터의 일반적인 패턴을 학습해 과적합을 방지할 수 있다.
- 데이터의 양이 적을 경우 의도적으로 기존의 데이터를 조금씩 변형, 추가하여 데이터를 늘린다. 이를 데이터 증식 또는 데이터 증강이라고 한다. 이미지의 경우 많이 사용됨
2. 모델의 복잡도 줄이기
- 인공 신경망의 복잡도는 은닉층의 수나 매개변수로 결정
- 은닉층을 줄여서 복잡도를 줄인다.
3. 가중치 규제(Regularization)적용
- 복잡한 모델이 간단한 모델보다 과적합될 가능성이 높음
- 간단한 모델은 적은 수의 매개변수를 가진 모델을 말함
- L1 규제 : 복잡한 모델을 좀 더 간단하게 하는 방법, 가중치 w들의 절대값 합계를 비용 함수에 추가함
- L2 규제 : 복잡한 모델을 좀 더 간단하게 하는 방법, 모든 가중치 w들의 제곱합을 비용 함수에 추가함
4. 드롭아웃(Dropout)
- 학습과정에서 신경망의 일부를 사용하지 않는 방법

09. 기울기 소실(Gradient Vanishing)과 폭주(Exploding)
- 기울기 소실: 딥러닝 중 역전파 과정에서 입력층으로 갈 수록 기울기가 점차 작아지는 현상이 발생할 수 있음, 입력층에서 가까운 층들에서 가중치 업데이트가 제대로 되지 않으면 결국 최적의 모델을 찾을 수 없는 것을 말함
- 기울기 폭주: 위와 반대의 경우로 기울기가 점차 커지다 가중치들이 비정상적으로 큰 값이 되면서 발산되는 것으로 순환신경망(Recurrent Neural Network, RNN)에서 발생 가능
1. ReLU와 ReLU의 변형들
- 기울기 소실을 완화하는 가장 간단한 방법은 은닉층 활성화 함수로 렐루나 렐루 변형 함수를 사용하는 것
2. 가중치 초기화(Weight initialization)
- 가중치 초기화만 적절히 해도 기울기 소실문제같은 것을 완화 가능
1. 세이비어 초기화(Xavier Initialization) or 글로럿 초기화(Glorot Initialization)
- 세이비어 초기화는 여러 층의 기울기 분산 사이에 균형을 맞춰 특정 층이 너무 주목받거나 다른 층이 뒤쳐지는 것을 막음
- 시그모이드, 하이퍼볼릭 탄젠트간은 S자 형태의 활성화 함수와 궁합이 좋음
- ReLU나 ReLU 변형 함수와는 궁합이 나쁨
2. He 초기화(He initialization)
- He 초기화는 세이비어 초기화와 다르게 다음 층의 뉴런의 수를 반영하지 않음
- ReLU 계열 함수를 사용할 경우에는 He 초기화 방법이 효율적
3. 배치 졍규화(Batch Nomalization)
- 배치 정규화는 인공 신경망의 각 층에 들어가는 입력을 평균과 분산으로 정규화해 학습을 효율적으로 만듬
1. 내부 공변량 변화(Internal Covariate Shihft)
- 학습 과정에서 층 별로 입력 데이터 분포가 달라지는 현상
2. 배치 정규화(Barch Normalization)
- 한 번에 들어오는 배치 단위로 정규화 하는 것을 말함
- 각 층에서 활성화 함수를 통과하기 전 수행
- 입력에 대해 평균을 0으로 만들고, 정규화를 한 뒤 정규화 된 데이터에 대해 스케일과 시프트를 수행함.
- 배치 정규화를 사용하면 시그모이드나 하이퍼볼릭탄젠트 함수를 사용하더라도 기울기 소실문제가 크게 개선됨
- 가중치 초기화에 훨씬 덜 민감해짐
- 훨씬 큰 학습률을 사용할 수 있어 학습 속도를 개선시킴
- 미니 배치마다 평균과 표준편차를 계산하므로 훈련데이터에 일종의 잡음을 넣는 부수효과로 과적합을 방지하는 효과가 있고, 드롭 아웃과 함께 사용하는 것이 좋음
- 모델을 복잡하게 하여 추가 계산을 하는 것이라 테스트 데이터에 대한 예측 시에 실행 시간이 느림, 서비스 속도를 고려한다면 배치 정규화가 필요한지 계산해봐야함
3. 배치 정규화의 한계
- 미니 배치 크기에 의존적, 작은 미니 배치에서는 배치 정규화의 효과가 극단적으로 작용되어 훈련에 악영향을 줄 수 있음
- RNN 에 적용하기 어려움
4. 층 정규화(Layer Normalization)
- RNN에 적용하는 것이 수월함
참고:
https://wikidocs.net/book/2788
PyTorch로 시작하는 딥 러닝 입문
이 책은 딥 러닝 프레임워크 PyTorch를 사용하여 딥 러닝에 입문하는 것을 목표로 합니다. 이 책은 2019년에 작성된 책으로 비영리적 목적으로 작성되어 출판 ...
wikidocs.net
'AI > PyTorch' 카테고리의 다른 글
| PyTorch #자연어 데이터 전처리 (0) | 2022.04.04 |
|---|---|
| PyTorch #합성곱 신경망(CNN) (0) | 2022.04.01 |
| PyTorch #소프트맥스 회귀(Softmax Regression) (0) | 2022.03.24 |
| PyTorch #로지스틱 회귀(Logistic Regression) (0) | 2022.03.23 |
| PyTorch #선형 회귀(Linear Regression) (0) | 2022.03.23 |



